Download demo source code HERE.
Terminator, matrix, i robot were all great movies because artifical intelligance is so cool concept. That's why humanity working hard to build a real skynet. Artifical neurol networks is a step forward on this purpose. It is a mathematical model of biological neurol networks. Unlike many humans, they can learn by experiance. Neurol network models can be trained by samples. A network is made of following structures.
- Input neurons: An input data for nerurol network to think about it.
- Neuron: A math function node that calculates inputs and genrates an output for other neurons. Output value is always must be a decimal between 0 and 1. Thats why functions like logistic or softmax usally prefered. Name of function that choosen for nerurons called "Activation Function".
- Hidden layers: Contains neurons that process input data. Mathematical magic happens here.
- Weights: Connections between neurons. They are just simple decimal numbers that sets characteristics of neurol network.
- Bias: Some value between 0 to 1 that added to neurons output. That prevents 0 valued outputs from neurons and keep neurons alive. Most boring thing in neurol networks.
- Output neurons: Final output and conclusion of your network.
Here is a visual represantation of ANN:
Artificial neural network is an application of mathematics so MATH IS THE MOST IMPORTANT PART! Let's take look at it step by step using graphic above. For each neuron in the hidden layers and output layer calculate output signals by following formula:
Here is an example of output signal calculation for a neuron called N1:
K is logistic sigmoid activation function of our neurons
gi is a vector of other connected neuron outputs and wi is vector of weight connections. Output signal function for each neuron is:
Every input data must be normalized to floating point between 0 to 1. That will also generate every neural signal in range of 0 to 1. This is the scaling equalization for input data:Here is an example of output signal calculation for a neuron called N1:
Output signal for N1=K(g1*w1+g2*w2+g3*w3)
Another example for output neuron called O1:
Output signal for O1=K(N1*w1+N2*2w+N3*w3+N4*w4)
We will get back to math later. That is enough for now. On this blog I will try to build an artificial neural network with .net and c# because there are enough python examples already. Also, I will try to do it on object oriented approach. It is simple to write it just using matrix calculations but I think this way is more easy to understand and maintain. Here is my object structure:
Layer class is a collection of neurons.
public class Layer { public Neuron[] Neurons { get; set; } }
Here is neuron class. We will breakdown all the details later.
public enum NeuronTypes { Input, Hidden, Output } public class Neuron { public List<Synapse> Inputs { get; set; } public List<Synapse> Outputs { get; set; } public double Output { get; set; } public double TargetOutput { get; set; } public double Delta { get; set; } public double Bias { get; set; } int? maxInput { get; set; } public NeuronTypes NeuronType { get; set; } public Neuron(NeuronTypes neuronType, int? maxInput) { this.NeuronType = neuronType; this.maxInput = maxInput; this.Inputs = new List<Synapse>(); this.Outputs = new List<Synapse>(); } public bool AcceptConnection { get { return !(NeuronType == NeuronTypes.Hidden && maxInput.HasValue && Inputs.Count > maxInput); } } public double InputSignal { get { return Inputs.Sum(d => d.Weight * (d.Source.Output + Bias)); } } public double BackwardSignal() { if (Outputs.Any()) { Delta = Outputs.Sum(d => d.Target.Delta * d.Weight) * activatePrime(Output); } else { Delta = (Output - TargetOutput) * activatePrime(Output); } return Delta + Bias; } public void AdjustWeights(double learnRate, double momentum) { if (Inputs.Any()) { foreach (var synp in Inputs) { var adjustDelta = Delta * synp.Source.Output; synp.Weight -= learnRate * adjustDelta + synp.PreDelta * momentum; synp.PreDelta = adjustDelta; } } } public double ForwardSignal() { Output = activate(InputSignal); return Output; } double activatePrime(double x) { return x * (1 - x); } double activate(double x) { return 1 / (1 + Math.Pow(Math.E, -x)); } }
Synapse class for connections between neurons.
public class Synapse { public double Weight { get; set; } public Neuron Target { get; set; } public Neuron Source { get; set; } public double PreDelta { get; set; } public double Gradient { get; set; } public Synapse(double weight, Neuron target, Neuron source) { Weight = weight; Target = target; Source = source; } }
And the NeuralNetwork class, the maestro that pulls them together.public class NeuralNetwork { public double LearnRate = .5; public double Momentum = .3; public List<Layer> Layers { get; private set; } int? maxNeuronConnection; public int? Seed { get; set; } public NeuralNetwork(int inputs, int[] hiddenLayers, int outputs, int? maxNeuronConnection = null, int? seed = null) { this.Seed = seed; this.maxNeuronConnection = maxNeuronConnection; this.Layers = new List<Layer>(); buildLayer(inputs, NeuronTypes.Input); for (int i = 0; i < hiddenLayers.Length; i++) { buildLayer(hiddenLayers[i], NeuronTypes.Hidden); } buildLayer(outputs, NeuronTypes.Output); InitSnypes(); } void buildLayer(int nodeSize, NeuronTypes neuronType) { var layer = new Layer(); var nodeBuilder = new List<Neuron>(); for (int i = 0; i < nodeSize; i++) { nodeBuilder.Add(new Neuron(neuronType, maxNeuronConnection)); } layer.Neurons = nodeBuilder.ToArray(); Layers.Add(layer); } private void InitSnypes() { var rnd = Seed.HasValue ? new Random(Seed.Value) : new Random(); for (int i = 0; i < Layers.Count - 1; i++) { var layer = Layers[i]; var nextLayer = Layers[i + 1]; foreach (var node in layer.Neurons) { node.Bias = 0.1 * rnd.NextDouble(); foreach (var nNode in nextLayer.Neurons) { if (!nNode.AcceptConnection) continue; var snypse = new Synapse(rnd.NextDouble(), nNode, node); node.Outputs.Add(snypse); nNode.Inputs.Add(snypse); } } } } public double GlobalError { get { return Math.Round(Layers.Last().Neurons.Sum(d => Math.Pow(d.TargetOutput - d.Output, 2) / 2), 4); } } public void BackPropagation() { for (int i = Layers.Count - 1; i > 0; i--) { var layer = Layers[i]; foreach (var node in layer.Neurons) { node.BackwardSignal(); } } for (int i = Layers.Count - 1; i >= 1; i--) { var layer = Layers[i]; foreach (var node in layer.Neurons) { node.AdjustWeights(LearnRate, Momentum); } } } public double[] Train(double[] _input, double[] _outputs) { if (_outputs.Count() != Layers.Last().Neurons.Count() || _input.Any(d => d < 0 || d > 1) || _outputs.Any(d => d < 0 || d > 1)) throw new ArgumentException(); var outputs = Layers.Last().Neurons; for (int i = 0; i < _outputs.Length; i++) { outputs[i].TargetOutput = _outputs[i]; } var result = FeedForward(_input); BackPropagation(); return result; } public double[] FeedForward(double[] _input) { if (_input.Count() != Layers.First().Neurons.Count()) throw new ArgumentException(); var InputLayer = Layers.First().Neurons; for (int i = 0; i < _input.Length; i++) { InputLayer[i].Output = _input[i]; } for (int i = 1; i < Layers.Count; i++) { var layer = Layers[i]; foreach (var node in layer.Neurons) { node.ForwardSignal(); } } return Layers.Last().Neurons.Select(d => d.Output).ToArray(); } }
Now lets take a look how this thing works. My simple goal is to give my network 2 inputs and expect average of them as output result. As I said before input data must be scaled to 0 to1 range. Of course I can simply calculate it like x=(a+b)/2. The point is a neural network can learn (almost) ANY function. It can LEARN any pattern. An ANN can be trained. For many cases this way is more effective than traditional methods. This approch works very well in vast area of applications like image recognition and processing, data classification, data prediction and of course artificial intelligence. Here is a console application sample:
class ANN { static void Main(string[] args) { var network = new NeuralNetwork(2, new int[] { 4 }, 1); var inputData = new double[] { .3, .5 }; var output = network.FeedForward(inputData); Console.Write("Inputs: {0} {1} Output:{2} ", inputData[0], inputData[1],output[0]); Console.ReadLine(); } }
new NeuralNetwork(2, new int[] { 4 }, 1); this means build neural network with 2 input neurons, 1 hidden layer with 4 neurons and 1 output neuron. .3 and .5 values sent towards network to generate an output signal by using FeedForward function. The result is:
Different values on every run:
What does it mean? We gave 0.3 and 0.5 as input data. Shouldn't we get 0.4 as an average of them? Yes computer science is modern sorcery but it is not that easy. We need to train our little ANN. We must teach what "average" means by showing samples over and over again. Before the learning part lets take a look at our artificial neural network deeper. What happened to data in ANN. On constructor method, layers built and neurons created in buildLayer. After that InitSnypes method created synapse connection layer by layer with some random value. That's why output result is different on each run. Every different structure generates a different output with same input. FeedForward calculates output signal using that connection values. What if there is an exact synapse connection build that generate average of my inputs as output. There are countless random combinations of these synapse weight values. How can we find the correct one? There is a mathe-magical spell to do this. It is called backpropagation. It is a common "supervised learning method" to train ANN's. An application of "Machine (deep) Learning". After output signal generated, if desired output is known we can calculate an error value and adjust the neural connection weights by backpropogation technique. Next time error should be smaller and smaller. After enough training error value will be ignorable. Let's train! Here is a windows form example.
public partial class Form1 : Form { public NeuralNetwork network; public List<double[]> trainingData; Random rnd; int trainedTimes; public Form1() { InitializeComponent(); //For debugging int Seed = 1923; // 2 input neurons 2 hidden layers with 3 and 2 neurons and 1 outpu neuron network = new NeuralNetwork(2, new int[] { 3, 3 }, 1, null, Seed); //Generate Random Training Data trainingData = new List<double[]>(); rnd = new Random(Seed); var trainingDataSize = 75; for (int i = 0; i < trainingDataSize; i++) { var input1 = Math.Round(rnd.NextDouble(), 2); //input 1 var input2 = Math.Round(rnd.NextDouble(), 2); // input 2 var output = (input1+input2)/2 ; // output as avarage of inputs trainingData.Add(new double[] { input1, input2, output });// Training data set chart1.Series[0].Points.AddXY(i, output); } } public void Train(int times) { //Train network x0 times for (int i = 0; i < times; i++) { //shuffle list for better training var shuffledTrainingData = trainingData.OrderBy(d => rnd.Next()).ToList(); List<double> errors = new List<double>(); foreach (var item in shuffledTrainingData) { var inputs = new double[] { item[0], item[1] }; var output = new double[] { item[2] }; //Train current set network.Train(inputs, output); errors.Add(network.GlobalError); } } chart1.Series[1].Points.Clear(); for (int i = 0; i < trainingData.Count; i++) { var set = trainingData[i]; chart1.Series[1].Points.AddXY(i, network.FeedForward(new double[] { set[0], set[1] })[0]); } trainedTimes += times; TrainCounterlbl.Text = string.Format("Trained {0} times", trainedTimes); } private void Trainx1_Click(object sender, EventArgs e) { Train(1); } private void Trainx50_Click(object sender, EventArgs e) { Train(50); } private void Trainx500_Click(object sender, EventArgs e) { Train(500); } private void TestBtn_Click(object sender, EventArgs e) { var testData = new double[] { rnd.NextDouble(), rnd.NextDouble() }; var result = network.FeedForward(testData)[0]; MessageBox.Show(string.Format("Input 1:{0} {4} Input 2:{1} {4} Expected:{3} Result:{2} {4}", format(testData[0]), format(testData[1]), format(result), format((testData[0]+ testData[1])/2), Environment.NewLine)); } string format(double val) { return val.ToString("0.000"); } }
Neural network has multiple hidden layers with 3 neurons each. 75 samples of random values generated at form constructor and stored in "trainingData". Here is the output chart of "trainingData".
When I press test data my untrained ANN thinks average of 0.316 and 0.339 is equals to 0.781
Press "Train X1" button to study every samples for one time and here is the result:
For each synapse connected to output neuron, backward signal can be calculated with following formula:
Net backward error signal for previous neuron can be calculated with following partial derivative respect to a weight.
Now let's inspect calculation of each term. The last term is error signal output of through a synapse connection.
For output neuron next term is simply actual output - expected output . (Yes that is why there is a 1/2 )After all backward signals calculated we need to adjust synapse weights for better results. α here is called momentum. It is an adjustment value for faster learning that represents previous value
In my code BackwardSignal applies partial derivative chain:
public double BackwardSignal() { if (Outputs.Any()) { Delta = Outputs.Sum(d => d.Target.Delta * d.Weight) * activatePrime(Output); } else { Delta = (Output - TargetOutput) * activatePrime(Output); } return Delta + Bias; }Then adjustment of weights at
public void AdjustWeights(double learnRate, double momentum) { if (Inputs.Any()) { foreach (var synp in Inputs) { var adjustDelta = Delta * synp.Source.Output; synp.Weight -= learnRate * adjustDelta + synp.PreDelta * momentum; synp.PreDelta = adjustDelta; } } }Back to demo application. Remember our application tries to find average of two input values. More we train better results we get. After training 50 times over artificial neural network, results begins to fit expected values.
100 training times later ANN fits far better.
Download demo source code HERE.












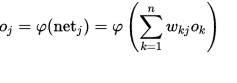






Hiç yorum yok:
Yorum Gönder